Tag: Trigonometry

10 Practice Questions for the Math Portion of the ACT

ACT math prep is essential for students looking to improve their scores and enhance their college applications. The ACT math section covers a variety of topics including algebra, geometry, trigonometry, and statistics. Effective preparation means not only practicing problems but also grasping the underlying concepts and mastering test-taking strategies. Using resources like practice questions, study guides, and prep bundles can help students identify their strengths and weaknesses. Consistent practice builds familiarity with the test format and can increase accuracy and speed. Teachers provide valuable support by offering guidance and resources to help students reach their highest potential

If you’re a teacher or a student gearing up for the math portion of the ACT, I’ve got just the thing for you—10 practice questions that mirror the ACT format with five multiple-choice options each. This set includes a mix of algebra, geometry, and probability to help gauge understanding and proficiency. An answer key is provided at the end to check the answers and see if students are on the right track. If more practice is needed, there’s a list of additional resources at the bottom of this post. Go ahead and take a look!

  1. What is the value of 3x2 – 5x + 2 when x = 2?
    A) 4
    B) 6
    C) 8
    D) 10
    E) 12
  2. In a right triangle, one angle measures 45 degrees. What is the measure of the other acute angle?
    A) 30 degrees
    B) 45 degrees
    C) 60 degrees
    D) 75 degrees
    E) 90 degrees
  3. Solve the equation: 2(x+1) = 16
    A) 2
    B) 3
    C) 4
    D) 5
    E) -2
  4. What is the area of a circle with a radius of 5 units?
    A) 15π square units
    B) 20π square units
    C) 25π square units
    D) 30π square units
    E) 35π square units
  5. Simplify the expression: √12⁄27
    A) √2⁄3
    B) √3⁄2
    C) 2⁄3
    D) 3⁄2
    E) Not Here
  6. If f(x) = 2x2 + 3x – 5, what is the value of f(4)?
    A) 17
    B) 23
    C) 29
    D) 35
    E) 39
  7. What is the y-value for the system of equations?
    2x + 3y = 7
    4x – y = 0
    A) y = 2
    B) y = 1
    C) y = 0
    D) y = -1
    E) y = 1⁄2
  8. A box contains 5 red balls, 4 blue balls, and 3 green balls. If one ball is randomly selected, what is the probability of selecting a blue ball?
    A) 1⁄3
    B) 1⁄2
    C) 4⁄11
    D) 3⁄10
    E) 8⁄9
  9. The sum of three consecutive even integers is 42. What is the smallest of the three integers?
    A) 10
    B) 12
    C) 14
    D) 16
    E) 18
  10. A triangle has side lengths of 5 cm, 8 cm, and 10 cm. What type of triangle is it?
    A) Equiangular triangle
    B) Acute triangle
    C) Obtuse triangle
    D) Right triangle
    E) Isosceles triangle

If you would like to have a PDF copy of these questions, then I will provide the link to the resource in my store. The store copy is slightly different. Question 4 has been changed to a higher difficulty and there are three bonus questions. The resource link is the last resource on this page. Scroll to the bottom.

Here’s an answer key with explanations:

  1. To find the value of the expression, substitute x = 2 into the expression:
    3(2)2 – 5(2) + 2 = 12 – 10 + 2 = 4
    Therefore, the answer is A) 4
  2. In a right triangle, one angle is always 90 degrees. The sum of the angles in a triangle is 180 degrees. Therefore, the measure of the other acute angle would be:
    180 – 90 – 45 = 45 degrees
    Therefore, the answer is B) 45 degrees.
  3. One way of solving this equation is turn 16 into 24, then set up the following equation and solve: 2(x+1) = 24 x+1 = 4 x = 3 Another way of solving this equation is by taking the logarithm (base 2) of both sides, we get:
    (x+1)log2(2) = log2(16)
    x+1 = log2(16)
    x+1 = 4
    x = 4 – 1
    x = 3
    Therefore, the answer is B) 3.
  4. The formula to find the area of a circle is A = πr2, where r is the radius. Substituting r = 5 into the formula, we get:
    A = π(5)2 = 25π square units
    Therefore, the answer is C) 25π square units.
  5. To simplify the expression, we need to find the square root of the fraction. Simplifying the fraction first, we get:
    √4⁄9
    Taking the square root of the numerator and denominator, we get:
    √4⁄9 = 2⁄3
    Therefore, the answer is C) 2⁄3.
  6. To find the value of f(4), substitute x = 4 into the function:
    f(4) = 2(4)2 + 3(4) – 5 = 32 + 12 – 5 = 39
    Therefore, the answer is E) 39.
  7. To solve the system of equations for y, we can use the method of substitution or elimination. By eliminating the variable x, we can find the value of y:
    Multiply the first equation by -2:
    -4x – 6y = -14
    4x – y = 0
    Add the two equations together:
    -7y = -14
    y = 2
    Therefore, the answer is A) y = 2.
  8. The probability of selecting a blue ball can be found by dividing the number of blue balls by the total number of balls:
    Probability = Number of blue balls / Total number of balls
    Probability = 4 / (5 + 4 + 3) = 4⁄12
    Simplifying the fraction, we get:
    Probability = 1⁄3
    Therefore, the answer is A) 1⁄3.
  9. Let’s assume the smallest even integer is x. The next two consecutive even integers would be x + 2 and x + 4. The sum of the three consecutive even integers is given as 42. Set up an equation:
    x + (x + 2) + (x + 4) = 42
    3x + 6 = 42
    3x = 36
    x = 12
    Therefore, the answer is B) 12
  10. Use Pythagorean Theorem to classify the triangle. If a2 + b2 = c2, then the triangle is a right triangle. If a2 + b2 > c2, then the triangle is an acute triangle. If a2 + b2 < c2, then the triangle is an obtuse triangle.
    52 = 25, 82 = 64 and 102 = 100
    25 + 64 < 100 or 89 < 100
    Therefore, the answer is C) Obtuse Triangle

Here’s a BONUS Question for Trig Practice that I grabbed out of my ACT 5 Week Test Prep:

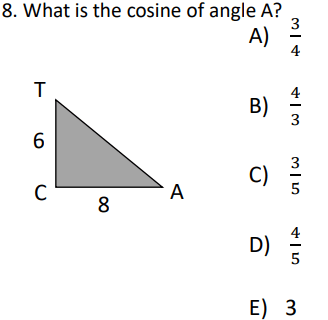
Students should remember SOH CAH TOA in order to tackle this problem. If the question asks for cosine, then look adjacent to A, which is 8, and then look at the hypotenuse, which does not have a measurement. Since TA needs a measurement, use the Pythagorean Theorem to find that the answer. 62 + 82 = TA2. Square the 6 and 8 then add them to get 100. The square root of 100 = 10, so TA = 10. Now, Cos(A) would be 8⁄10 and would reduce to 4⁄5, which is answer choice D.

I hope these practice questions prove helpful. Consistent practice is key to improving skills and boosting confidence for the ACT. For additional resources, check out the links provided. Good luck on preparing!

All these individual resources are part of the ACT Math Success Prep Bundle. Whether you need to focus on specific objectives or want comprehensive practice, I’ve got your covered.

Trigonometry for the Geometry Classroom

It’s finally trig time! Yay! I love trig. Students tend to enjoy it too because it is so different from everything they have been taught so far. Over the years, I’ve tried different approaches to teaching trig. I know what kids struggle on and I finally feel like I’ve got a good way of teaching it. I see my trig unit broken into these parts:

  • Intro to Trig
  • Practice Finding Opposite, Hypotenuse and Adjacent
  • Setting Up Problems and Solving Them
  • Practice
  • Review
  • Assessment
  • More Assessment

Trig can be simple but to some students it can be complicated. They actually love it once they get the hang of it and how fun is it to use the calculator this much?! (When I first learned trig, we used charts to find the answers. We did not have calculators that would do the calculations. Yes, I’m old!)

When I created this unit, I knew what the two main issues were with teaching trig: 1) Teaching them which trig function to use 2) Teaching them how to solve the different types of problems

I decided to work backwards a little. In my introduction, I just tell them (As Bill and Ted would say) we are about to embark on an excellent adventure called Trig. I introduce a right triangle and tell them to visualize that they are in a right triangular room. They are sitting in one of the corners (not the right angle). I go on to talk about where opposite is and how when you are sitting in the corner, you can touch the hypotenuse and adjacent sides at the same time, but you can’t reach the opposite side. There are some notes we take and then we play a dice game.

For the dice game, I usually get my first class to cut out and put together the dice. Now I have the dice for the rest of the day. I put students into groups of 3 or 4 and they are competing against the rest of the class. There are three dice. One with triangles, one with dots and one with the words, hypotenuse, opposite and adjacent. Click the link below to watch the dice game which practices knowing the different sides with respect to a certain angle. Dice Game Short Video.

Before going any further, I teach kids SOH CAH TOA and we do some practice on finding those ratios. That part is normal progression, but here is the part that might seem a little backwards: I teach them how to solve trig equations next! The students do not know how to set them up yet, but I have figured out that if I go ahead and teach them how to solve the equations, then once they start setting them up, solving is a breeze. I teach them how to solve these three types of problems:

  • Looking for an angle
  • Looking for a side and the x is in the numerator
  • Looking for a side and the x is in the denominator

By the way, when teaching them how to solve these problem, get them to completely solve for x before typing anything into the calculator. Don’t let them find the sin of an angle, then multiply by the side. Let them type the whole thing in: 12 sin(36). I like this method because then the students aren’t rounding answers until the end of the problem. You can see that I did that in the examples above in problems 5 & 6.

Next is the PowerPoint. In the picture to the right, you can see one of the slides in the PowerPoint. Only the triangle with the sun, and the two arrows appear and students have to name which trig function is being referenced. I don’t use degrees for a while, I’ll just use symbols. I don’t want the variables and numbers to get in the way. Toward the end of the PowerPoint, the students are asked to set up the problems and then at the end, they go back to solve them.

Now it’s time to practice. I have 3 worksheets that help students find missing sides and angles. The first one places only an x on one side, a number on a side and gives one angle. This makes it easy to determine the trig function and it is like the PowerPoint. The next worksheet gives the students two sides and asks them to find the missing angle. The last worksheet is the toughest because now the students have to find x, y and z… two sides and an angle. This is much more difficult because it will not be obvious from the start which trig function to use. Students need to see that they actually have a choice sometimes and they need to decide where to start and ignore the extra info. I also throw in some special right triangles and an right triangle altitude problem to see if they remember those rules. The PowerPoint from earlier brings up that there might be more than one way to solve a problem, so hopefully when they get to the worksheet, they will use a quick special right triangle rule instead of trig, but if they can find the answer either way, I’m happy.

I have another resource that is not in this trig unit that I do at this point. It’s the Trig Maze. The students really get into it and work at it. It’s cool to work a problem and then see your answer on the paper (they are thinking, “YAY, I did it right!”) and it’s even cooler that it leads you to the next problem you are supposed to work. The maze comes with an answer document, so you can see all of their work!

Finally, I like to do some task cards with some real-life situations. Some of the task cards contain a ladder against a building, finding a flagpole height, finding the diagonal in a rectangle etc. There are 12 of these problems.

I end the unit with what I call the “Poodle Problem”. It is a group of 5 triangles that have been put together to look like a poodle. Go back and look at the very first picture at the top of this blog. That’s the Poodle Problem! The students find all the answers, then total them for one final answer. How fast is this to grade? Super fast! It’s a great quiz and a great end to the unit.

I’m not finished yet! Now I like to test all of the right triangle content. I have a test that I call the Right Triangle Test that has 10 questions with the following problems:

  • One Pythagorean Theorem Problem where they have to find the perimeter of the triangle.
  • One Right Triangle Altitude Problem where they have to find the perimeter of the triangle.
  • One 30-60-90 Problem where they have to find the area of the triangle.
  • One 45-45-90 Problem – easy, they just find the hypotenuse
  • Six Trig Problems – Just find a missing side, except for one problem is like the task cards, but a little tougher.

I had problems with cheating one year, so I went crazy and made 5 versions of the same test. You even have a choice of an answer bank or no answer bank. One of the 5 tests is a shortened version that I’ve used as a retest or a modified test. (It gives the students a little help on setting up some of the problems too.) I don’t like to give long tests. Students get enough testing. I like tests that are short and to the point. As long as I can tell they “get it”, why does it have to be super long?

I’m very happy with this unit. The only thing that it doesn’t contain right now is angle of elevation and depression problems. I’ll try to add this to the unit this summer. These problems were a big deal at one time, but it seems like we’ve gotten away from them in Geometry. I still think it’s good for students to see them.

Trig is fun and different and essential to future math classes. Below is all of my right triangle lessons including the Trig resource I’ve been talking about. What’s next on my agenda after right triangle trig? Law of Sines and Cosines of course! Law of Sines and Cosines is sold separately in my store, but it is also a part of Unit 7 below.