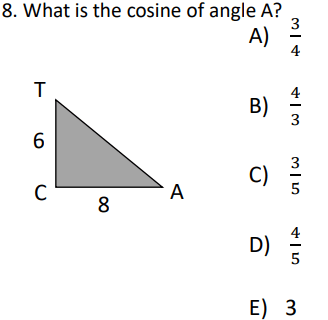Tag: mathematics

Points of Concurrency: Connecting Geometry & Algebra

As educators, we’re always juggling – trying to cover a mountain of curriculum while making sure our students really understand the core concepts. And sometimes, we stumble upon those topics that make us wonder, “Is this really essential?” Points of concurrency and special segments in triangles often fall into this category. They can seem a bit intimidating, and let’s face it, we’re often pressed for time. So, should we teach them? Skim them? Skip them entirely?

Let’s explore this geometric puzzle, considering curriculum needs, the value of these concepts, and some practical strategies for teaching them effectively.

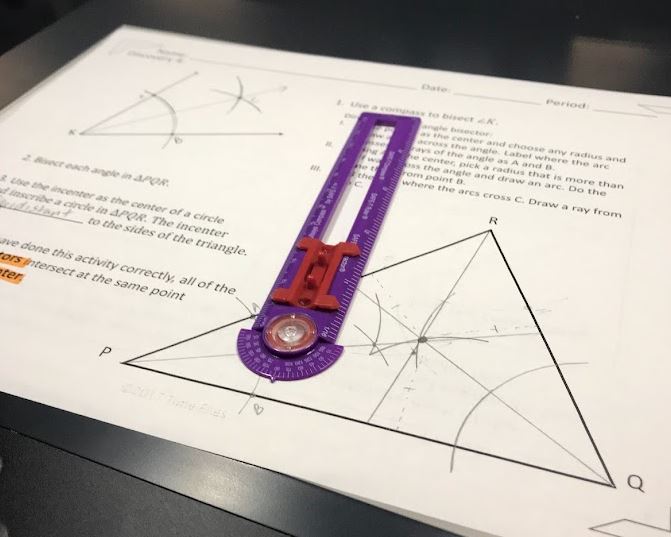
Why These Concepts Matter

Points of concurrency (like the centroid, incenter, circumcenter, and orthocenter) and their related segments (medians, angle bisectors, perpendicular bisectors, and altitudes) are more than just geometric trivia. They deepen students’ understanding of triangles and provide a fantastic opportunity to reinforce essential algebra and coordinate geometry skills.

Think about it: Finding midpoints to construct medians? That’s a direct link to the midpoint formula! Exploring perpendicular bisectors? Hello, slope and linear equations! These connections help students see the bigger picture of math, where different concepts intertwine and support each other.

To Teach or Not to Teach…That is the Question!

Of course, before diving in, it’s crucial to check your state’s curriculum requirements. Texas educators, you’re in luck – these topics are explicitly included in your standards. But that’s not the case everywhere. Even if these concepts aren’t mandated, incorporating them (even in a simplified way) can enrich your students’ geometric understanding and strengthen those all-important algebra connections.

Time-Saving Strategies for Busy Teachers

Okay, let’s be real. We’re all short on time. If you’re feeling the curriculum crunch, here’s how to approach these concepts efficiently:

  • Keep it concise: Focus on definitions, basic constructions, key properties, and simple applications. No need to get lost in the weeds!
  • Link it to algebra: Highlight those connections to the midpoint formula, slope, etc. – it’s built-in review!
  • Get hands-on: Ditch the lengthy lectures and opt for interactive activities. Dynamic geometry software like GeoGebra or Desmos is your friend!

Quick Activity Ideas:

  • Software exploration: Let students construct triangles and explore those points of concurrency virtually.
  • “Find the Center” challenge: Give clues about a specific point of concurrency and have students play detective.
  • Real-world connections: Briefly touch on how these concepts are used in architecture or engineering.

By keeping it focused and engaging, you can make these concepts accessible even with limited time.

Beyond Geometry: Expanding the Horizons

Here’s the cool thing about points of concurrency and special segments: they can bridge the gap between different math topics. Imagine your Algebra 2 students revisiting systems of equations through the lens of triangle properties. Or your geometry students solidifying their coordinate geometry skills. It’s all about making connections and deepening understanding.

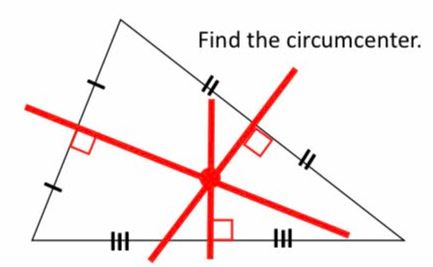
Ready for a Deep Dive?

While simplifying is helpful, sometimes you want to go deeper. If you’re looking for a comprehensive and engaging resource, check out “Points of Concurrency Lesson and Project.” This resource provides hands-on activities, real-world applications, and a chance to reinforce those crucial algebra skills. It’s a fantastic way to provide a more in-depth and enriching learning experience.

Wrapping It Up

Whether you simplify, integrate, or (occasionally) skip, remember that a well-rounded mathematical education is key. Points of concurrency and special segments, while sometimes overlooked, offer valuable learning opportunities. By approaching them thoughtfully, you can equip your students with the skills they need to succeed in their mathematical journeys.extend beyond the classroom.

10 Practice Questions for the Math Portion of the ACT

ACT math prep is essential for students looking to improve their scores and enhance their college applications. The ACT math section covers a variety of topics including algebra, geometry, trigonometry, and statistics. Effective preparation means not only practicing problems but also grasping the underlying concepts and mastering test-taking strategies. Using resources like practice questions, study guides, and prep bundles can help students identify their strengths and weaknesses. Consistent practice builds familiarity with the test format and can increase accuracy and speed. Teachers provide valuable support by offering guidance and resources to help students reach their highest potential

If you’re a teacher or a student gearing up for the math portion of the ACT, I’ve got just the thing for you—10 practice questions that mirror the ACT format with five multiple-choice options each. This set includes a mix of algebra, geometry, and probability to help gauge understanding and proficiency. An answer key is provided at the end to check the answers and see if students are on the right track. If more practice is needed, there’s a list of additional resources at the bottom of this post. Go ahead and take a look!

  1. What is the value of 3x2 – 5x + 2 when x = 2?
    A) 4
    B) 6
    C) 8
    D) 10
    E) 12
  2. In a right triangle, one angle measures 45 degrees. What is the measure of the other acute angle?
    A) 30 degrees
    B) 45 degrees
    C) 60 degrees
    D) 75 degrees
    E) 90 degrees
  3. Solve the equation: 2(x+1) = 16
    A) 2
    B) 3
    C) 4
    D) 5
    E) -2
  4. What is the area of a circle with a radius of 5 units?
    A) 15π square units
    B) 20π square units
    C) 25π square units
    D) 30π square units
    E) 35π square units
  5. Simplify the expression: √12⁄27
    A) √2⁄3
    B) √3⁄2
    C) 2⁄3
    D) 3⁄2
    E) Not Here
  6. If f(x) = 2x2 + 3x – 5, what is the value of f(4)?
    A) 17
    B) 23
    C) 29
    D) 35
    E) 39
  7. What is the y-value for the system of equations?
    2x + 3y = 7
    4x – y = 0
    A) y = 2
    B) y = 1
    C) y = 0
    D) y = -1
    E) y = 1⁄2
  8. A box contains 5 red balls, 4 blue balls, and 3 green balls. If one ball is randomly selected, what is the probability of selecting a blue ball?
    A) 1⁄3
    B) 1⁄2
    C) 4⁄11
    D) 3⁄10
    E) 8⁄9
  9. The sum of three consecutive even integers is 42. What is the smallest of the three integers?
    A) 10
    B) 12
    C) 14
    D) 16
    E) 18
  10. A triangle has side lengths of 5 cm, 8 cm, and 10 cm. What type of triangle is it?
    A) Equiangular triangle
    B) Acute triangle
    C) Obtuse triangle
    D) Right triangle
    E) Isosceles triangle

If you would like to have a PDF copy of these questions, then I will provide the link to the resource in my store. The store copy is slightly different. Question 4 has been changed to a higher difficulty and there are three bonus questions. The resource link is the last resource on this page. Scroll to the bottom.

Here’s an answer key with explanations:

  1. To find the value of the expression, substitute x = 2 into the expression:
    3(2)2 – 5(2) + 2 = 12 – 10 + 2 = 4
    Therefore, the answer is A) 4
  2. In a right triangle, one angle is always 90 degrees. The sum of the angles in a triangle is 180 degrees. Therefore, the measure of the other acute angle would be:
    180 – 90 – 45 = 45 degrees
    Therefore, the answer is B) 45 degrees.
  3. One way of solving this equation is turn 16 into 24, then set up the following equation and solve: 2(x+1) = 24 x+1 = 4 x = 3 Another way of solving this equation is by taking the logarithm (base 2) of both sides, we get:
    (x+1)log2(2) = log2(16)
    x+1 = log2(16)
    x+1 = 4
    x = 4 – 1
    x = 3
    Therefore, the answer is B) 3.
  4. The formula to find the area of a circle is A = πr2, where r is the radius. Substituting r = 5 into the formula, we get:
    A = π(5)2 = 25π square units
    Therefore, the answer is C) 25π square units.
  5. To simplify the expression, we need to find the square root of the fraction. Simplifying the fraction first, we get:
    √4⁄9
    Taking the square root of the numerator and denominator, we get:
    √4⁄9 = 2⁄3
    Therefore, the answer is C) 2⁄3.
  6. To find the value of f(4), substitute x = 4 into the function:
    f(4) = 2(4)2 + 3(4) – 5 = 32 + 12 – 5 = 39
    Therefore, the answer is E) 39.
  7. To solve the system of equations for y, we can use the method of substitution or elimination. By eliminating the variable x, we can find the value of y:
    Multiply the first equation by -2:
    -4x – 6y = -14
    4x – y = 0
    Add the two equations together:
    -7y = -14
    y = 2
    Therefore, the answer is A) y = 2.
  8. The probability of selecting a blue ball can be found by dividing the number of blue balls by the total number of balls:
    Probability = Number of blue balls / Total number of balls
    Probability = 4 / (5 + 4 + 3) = 4⁄12
    Simplifying the fraction, we get:
    Probability = 1⁄3
    Therefore, the answer is A) 1⁄3.
  9. Let’s assume the smallest even integer is x. The next two consecutive even integers would be x + 2 and x + 4. The sum of the three consecutive even integers is given as 42. Set up an equation:
    x + (x + 2) + (x + 4) = 42
    3x + 6 = 42
    3x = 36
    x = 12
    Therefore, the answer is B) 12
  10. Use Pythagorean Theorem to classify the triangle. If a2 + b2 = c2, then the triangle is a right triangle. If a2 + b2 > c2, then the triangle is an acute triangle. If a2 + b2 < c2, then the triangle is an obtuse triangle.
    52 = 25, 82 = 64 and 102 = 100
    25 + 64 < 100 or 89 < 100
    Therefore, the answer is C) Obtuse Triangle

Here’s a BONUS Question for Trig Practice that I grabbed out of my ACT 5 Week Test Prep:

Students should remember SOH CAH TOA in order to tackle this problem. If the question asks for cosine, then look adjacent to A, which is 8, and then look at the hypotenuse, which does not have a measurement. Since TA needs a measurement, use the Pythagorean Theorem to find that the answer. 62 + 82 = TA2. Square the 6 and 8 then add them to get 100. The square root of 100 = 10, so TA = 10. Now, Cos(A) would be 8⁄10 and would reduce to 4⁄5, which is answer choice D.

I hope these practice questions prove helpful. Consistent practice is key to improving skills and boosting confidence for the ACT. For additional resources, check out the links provided. Good luck on preparing!

All these individual resources are part of the ACT Math Success Prep Bundle. Whether you need to focus on specific objectives or want comprehensive practice, I’ve got your covered.