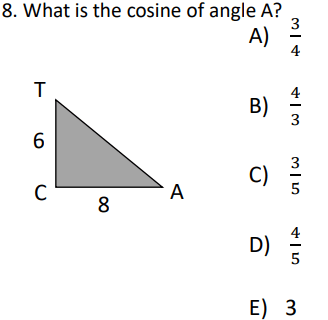Category: Math

30 Ways to Say “Show Your Work” (Without Saying “Show Your Work”)

If you’ve ever told a student to show their work and been met with blank stares, scribbled-down numbers, or complete avoidance, you’re not alone. The truth is, many students don’t actually know what show your work means—or why it matters. To them, it sounds like just another rule, a hoop to jump through. But what if we reframed it?

The key is helping students see that showing their work isn’t about writing things down just because we said so—IT’S ABOUT MAKING THEIR THINKING VISIBLE! It’s about leaving a trail so they can check their reasoning, catch mistakes, and explain their process. And sometimes, the phrase show your work just doesn’t connect.

So, let’s rethink the way we ask students to document their thinking. Here are 30 different ways to say ‘show your work’ that might resonate more with your students:

Process-Oriented Phrases

  1. Document your thinking.
  2. Make mathematical notes.
  3. Write down your thought process.
  4. Track your steps.
  5. Show how you figured it out.
  6. Record your strategy.
  7. Map out your solution.
  8. Make your thinking visible.
  9. Break it down step by step.
  10. Illustrate your reasoning.

Student-Centered Language

  1. Convince me your answer makes sense.
  2. Tell the story of how you solved it.
  3. What would you write to teach someone else?
  4. Create a roadmap for your brain.
  5. Explain your approach in a way a friend would understand.
  6. Help me see what’s going on in your head.
  7. Write it in a way future-you will understand when you check your work.
  8. If you got stuck, what steps did you take before that?
  9. How can you prove your answer is correct?
  10. Would someone else be able to follow your thinking?

Visual/Creative Approaches

  1. Sketch your solution.
  2. Draw a diagram to support your answer.
  3. Use arrows or highlights to show key steps.
  4. Make a quick explainer box.
  5. Write a one-minute summary of what you did.
  6. Turn it into a “math comic strip.”
  7. Use colors to separate different parts of your thinking.
  8. Write a math journal entry about this problem.
  9. Make a checklist of the steps you took.
  10. Explain it in a way you’d post on social media (but keep it math-related!).

Why This Matters

When students hear show your work, they often think we’re asking for a long, tedious process that just slows them down. But when we shift the language to focus on thinking, reasoning, and problem-solving, it becomes more meaningful.

Try using some of these alternative phrases in your classroom and see how your students respond. You might just find that showing their work becomes something they actually understand—and maybe even value.

What are your favorite ways to get students to document their thinking? Do you like any of the ones above? Share in the comments!

Bell ringers are a great place to have students demonstrate they know how to show work or make their reasoning visible. The bundle below has 144 days-worth of bell work problems. Click on the resource to see more details.

Easy-to-Use SAT Math Practice Sheets for Teachers and Students

Did you know that the average SAT math score is barely above 500 the past few years? Preparing for the SAT Math Test can feel overwhelming for both students and teachers. With so much content to cover, finding resources that are comprehensive, easy to use, and effective is essential. That’s why I’ve created my SAT Math Practice Sets—a collection of worksheets designed to target the key areas tested on the SAT. These practice sheets are a powerful tool for students preparing for test day and for teachers looking to build confidence and skills in their classrooms.

What Are the SAT Math Practice Sets?

Each SAT Math Practice Set contains six worksheets with carefully curated problems that align with the four categories tested on the SAT Math section:

  • Algebra: Linear equations, systems of equations, and quadratic functions.
  • Advanced Math: Polynomials, rational expressions, and nonlinear systems.
  • Problem Solving & Data Analysis: Data interpretation, probability, and real-world applications.
  • Geometry & Trigonometry: Triangles, circles, volume, and trigonometric ratios.

The problems range in difficulty, from basic to advanced, mimicking the progression of questions students will face on the test. Each worksheet includes a mix of multiple-choice and free-response questions to provide a well-rounded practice experience.

What Makes These Practice Sets Special?

  1. Detailed Answer Keys: Each set includes step-by-step solutions for every question. This helps students learn from their mistakes and ensures teachers can easily guide their students through challenging problems.
  2. Error Analysis: Students are encouraged to reflect on their errors, identify patterns in their mistakes, and learn strategies to avoid them in the future.
  3. Test-Like Practice: The questions are formatted and styled after real SAT questions, so students can familiarize themselves with the test’s structure.
  4. Progressive Difficulty: Each worksheet increases in difficulty, helping students build confidence as they master foundational skills and tackle more advanced concepts.

How to Use These Practice Sets

Here are a few ways you can use the SAT Math Practice Sets in your classroom or at home:

  1. Daily Warm-Ups: Start each class with a few problems to get students thinking critically and practicing consistently.
  2. Weekly Homework: Assign one worksheet per week to keep students on track with their SAT prep.
  3. Group Activities: Have students work in small groups to solve problems and present their solutions to the class.
  4. Tutoring Sessions: Use these sheets during SAT prep sessions to target specific areas where students need improvement.
  5. Self-Paced Practice: Encourage students to work through the sheets at their own pace, using the answer keys and error analysis sections to guide their learning.

Why SAT Math Practice Matters

Success on the SAT Math Test isn’t just about knowing formulas and equations. It’s about developing problem-solving skills, understanding how to approach different question types, and managing time effectively. These practice sets are designed to help students build those skills while giving teachers an easy-to-implement resource to support their instruction. Here are the sets that I’ve made so far: SET 1 and SET 2.

What’s Next?

I’m working on additional practice sets to expand the collection. My goal is to provide even more targeted practice for specific topics and introduce new question formats to align with the digital SAT. Stay tuned for updates and new resources!

Whether you’re a teacher helping students prepare for college entrance exams or a student working toward your best score, these SAT Math Practice Sets are here to make the journey easier and more effective. Check them out today and see the difference they can make in your SAT prep!

Have questions or suggestions? Drop them in the comments below—I’d love to hear how you’re using these resources in your classroom or at home!

10 Practice Questions for the Math Portion of the ACT

ACT math prep is essential for students looking to improve their scores and enhance their college applications. The ACT math section covers a variety of topics including algebra, geometry, trigonometry, and statistics. Effective preparation means not only practicing problems but also grasping the underlying concepts and mastering test-taking strategies. Using resources like practice questions, study guides, and prep bundles can help students identify their strengths and weaknesses. Consistent practice builds familiarity with the test format and can increase accuracy and speed. Teachers provide valuable support by offering guidance and resources to help students reach their highest potential

If you’re a teacher or a student gearing up for the math portion of the ACT, I’ve got just the thing for you—10 practice questions that mirror the ACT format with five multiple-choice options each. This set includes a mix of algebra, geometry, and probability to help gauge understanding and proficiency. An answer key is provided at the end to check the answers and see if students are on the right track. If more practice is needed, there’s a list of additional resources at the bottom of this post. Go ahead and take a look!

  1. What is the value of 3x2 – 5x + 2 when x = 2?
    A) 4
    B) 6
    C) 8
    D) 10
    E) 12
  2. In a right triangle, one angle measures 45 degrees. What is the measure of the other acute angle?
    A) 30 degrees
    B) 45 degrees
    C) 60 degrees
    D) 75 degrees
    E) 90 degrees
  3. Solve the equation: 2(x+1) = 16
    A) 2
    B) 3
    C) 4
    D) 5
    E) -2
  4. What is the area of a circle with a radius of 5 units?
    A) 15π square units
    B) 20π square units
    C) 25π square units
    D) 30π square units
    E) 35π square units
  5. Simplify the expression: √12⁄27
    A) √2⁄3
    B) √3⁄2
    C) 2⁄3
    D) 3⁄2
    E) Not Here
  6. If f(x) = 2x2 + 3x – 5, what is the value of f(4)?
    A) 17
    B) 23
    C) 29
    D) 35
    E) 39
  7. What is the y-value for the system of equations?
    2x + 3y = 7
    4x – y = 0
    A) y = 2
    B) y = 1
    C) y = 0
    D) y = -1
    E) y = 1⁄2
  8. A box contains 5 red balls, 4 blue balls, and 3 green balls. If one ball is randomly selected, what is the probability of selecting a blue ball?
    A) 1⁄3
    B) 1⁄2
    C) 4⁄11
    D) 3⁄10
    E) 8⁄9
  9. The sum of three consecutive even integers is 42. What is the smallest of the three integers?
    A) 10
    B) 12
    C) 14
    D) 16
    E) 18
  10. A triangle has side lengths of 5 cm, 8 cm, and 10 cm. What type of triangle is it?
    A) Equiangular triangle
    B) Acute triangle
    C) Obtuse triangle
    D) Right triangle
    E) Isosceles triangle

If you would like to have a PDF copy of these questions, then I will provide the link to the resource in my store. The store copy is slightly different. Question 4 has been changed to a higher difficulty and there are three bonus questions. The resource link is the last resource on this page. Scroll to the bottom.

Here’s an answer key with explanations:

  1. To find the value of the expression, substitute x = 2 into the expression:
    3(2)2 – 5(2) + 2 = 12 – 10 + 2 = 4
    Therefore, the answer is A) 4
  2. In a right triangle, one angle is always 90 degrees. The sum of the angles in a triangle is 180 degrees. Therefore, the measure of the other acute angle would be:
    180 – 90 – 45 = 45 degrees
    Therefore, the answer is B) 45 degrees.
  3. One way of solving this equation is turn 16 into 24, then set up the following equation and solve: 2(x+1) = 24 x+1 = 4 x = 3 Another way of solving this equation is by taking the logarithm (base 2) of both sides, we get:
    (x+1)log2(2) = log2(16)
    x+1 = log2(16)
    x+1 = 4
    x = 4 – 1
    x = 3
    Therefore, the answer is B) 3.
  4. The formula to find the area of a circle is A = πr2, where r is the radius. Substituting r = 5 into the formula, we get:
    A = π(5)2 = 25π square units
    Therefore, the answer is C) 25π square units.
  5. To simplify the expression, we need to find the square root of the fraction. Simplifying the fraction first, we get:
    √4⁄9
    Taking the square root of the numerator and denominator, we get:
    √4⁄9 = 2⁄3
    Therefore, the answer is C) 2⁄3.
  6. To find the value of f(4), substitute x = 4 into the function:
    f(4) = 2(4)2 + 3(4) – 5 = 32 + 12 – 5 = 39
    Therefore, the answer is E) 39.
  7. To solve the system of equations for y, we can use the method of substitution or elimination. By eliminating the variable x, we can find the value of y:
    Multiply the first equation by -2:
    -4x – 6y = -14
    4x – y = 0
    Add the two equations together:
    -7y = -14
    y = 2
    Therefore, the answer is A) y = 2.
  8. The probability of selecting a blue ball can be found by dividing the number of blue balls by the total number of balls:
    Probability = Number of blue balls / Total number of balls
    Probability = 4 / (5 + 4 + 3) = 4⁄12
    Simplifying the fraction, we get:
    Probability = 1⁄3
    Therefore, the answer is A) 1⁄3.
  9. Let’s assume the smallest even integer is x. The next two consecutive even integers would be x + 2 and x + 4. The sum of the three consecutive even integers is given as 42. Set up an equation:
    x + (x + 2) + (x + 4) = 42
    3x + 6 = 42
    3x = 36
    x = 12
    Therefore, the answer is B) 12
  10. Use Pythagorean Theorem to classify the triangle. If a2 + b2 = c2, then the triangle is a right triangle. If a2 + b2 > c2, then the triangle is an acute triangle. If a2 + b2 < c2, then the triangle is an obtuse triangle.
    52 = 25, 82 = 64 and 102 = 100
    25 + 64 < 100 or 89 < 100
    Therefore, the answer is C) Obtuse Triangle

Here’s a BONUS Question for Trig Practice that I grabbed out of my ACT 5 Week Test Prep:

Students should remember SOH CAH TOA in order to tackle this problem. If the question asks for cosine, then look adjacent to A, which is 8, and then look at the hypotenuse, which does not have a measurement. Since TA needs a measurement, use the Pythagorean Theorem to find that the answer. 62 + 82 = TA2. Square the 6 and 8 then add them to get 100. The square root of 100 = 10, so TA = 10. Now, Cos(A) would be 8⁄10 and would reduce to 4⁄5, which is answer choice D.

I hope these practice questions prove helpful. Consistent practice is key to improving skills and boosting confidence for the ACT. For additional resources, check out the links provided. Good luck on preparing!

All these individual resources are part of the ACT Math Success Prep Bundle. Whether you need to focus on specific objectives or want comprehensive practice, I’ve got your covered.

What Unfolds in Your Math Class When the Bell Rings?

The bell to start class just rang. Now what? Let’s talk about those classroom openers that go by many names – “bell ringers”, “warm ups”, or “do nows”. After over 35 years in the teaching game, I’ve had my fair share of experiences with these little classroom kickstarters. You could say that bell ringers (or your preferred name) and I have a bit of a “frenemy” relationship. Why? Let me elaborate on the advantages and challenges I’ve experienced with bell ringers throughout my career.

As we head into a new school year, I’ve been thinking about what still works — and what needs a refresh. Bell ringers are one of those things that can either work for you or they can be a challenge. It’s important to know how to use them properly and to realize the purpose.

The Value of Bell Ringers

First things first, let’s acknowledge the credit bell ringers deserve. They can truly elevate your teaching game. Once seamlessly integrated into your daily flow, most students will fall in line. When students enter the room, they dive straight into the bell ringer activity. This gives you some precious moments to tackle all those initial tasks that need attention – like attendance, catching up with absentees, and the never-ending quest for missing assignments.

Wondering how to make this streamlined approach a reality? It’s all about setting the groundwork from day one. Here’s the deal: let your students know that the next time they walk into the classroom, there will be a bell ringer or directions on the board waiting for them, and they should start on it right away. Consistency is key here – when you establish this routine early on, students will come to expect it and know exactly what’s coming their way.

But that’s not all. Having them dive into the bell ringer gets their gears turning. It’s like flipping a switch that says, “Time to learn, folks!” The activity itself helps reel in their focus, and guess what? It prevents those precious minutes from vanishing into thin air. Trust me, math teachers know how to squeeze every ounce of learning time from the clock.

What adds to the charm of bell ringers is their versatility. They can serve specific purposes within your lesson plan. Whether reviewing a topic, accessing material that might otherwise be overlooked, or even acting as a captivating lesson hook – a purpose-driven bell ringer provides valuable insights to educators while aiding students’ comprehension of topics and sparking their interest.

I often used bell ringers to prepare students for upcoming exams such as in-school ACT, SAT, or state tests. Additionally, I found value in conducting reviews of past topics and addressing areas where I knew many students have learning gaps.

Let’s Talk Challenges Now

It’s important to know that bell ringers don’t always go as planned. One big issue is treating them as just something to pass the time. If students think they’re not important, they might not take them seriously. Have you ever had a student ask, “Does this count for a grade?” That’s their way of saying, “I’ll only do it if it matters.” So, the trick is to make sure they have a clear purpose. Even if grades aren’t involved, helping students understand how the bell ringer helps their learning is key. It is also important that students know that once they are finished with the bell ringer, there’s a good chance that someone in the room will have to explain how to work the problem or even go to the board and work it. If students feel like they might get called on, they will not want to get caught off guard.

There were times when I was in a pinch and had to create a bell ringer on the fly, without much preparation. It’s no secret that students can sense when things are a bit disorganized. You see, the whole “Fake it until you make it” idea doesn’t work well in teaching. You can’t pretend to be organized. With a classroom full of around 28 students, there’s just too much happening. You’ve got to be on your A-game. Teaching requires real organization and being genuinely ready for what’s ahead. So, take it from someone who’s been through it – staying organized is a true game-changer and that applies to having a prepared bell ringer.

There have been times when I decided to stop doing bell ringers altogether, or at least in some classes. During remote learning, my bell ringers didn’t translate well online, so I paused them for a while. The important thing is, it’s okay to change things up when needed.

Transitioning from one activity to another can make or break the classroom atmosphere. There were years when after the bell ringer, things got a bit crazy until I could get things back on track. Realizing the importance of fewer disruptions in certain classes, I chose to skip bell ringers to stay focused and keep my sanity intact. By the way, transitions can be smooth. If you give clear directions on what to do next and even set a timer, they can go better.

The biggest reason that I have a love-hate relationship with bell ringers is the significant time investment required to either source or craft them. It can feel counterintuitive to dedicate an hour to creating something that’s intended to occupy just around 10 minutes or less of valuable class time.

Purpose Matters

If you’re set on doing bell ringers, give them a purpose. Before going any further on your quest for bell ringers, stop and write the purpose the bell ringer will serve. Here are some suggestions:

  • It will be a hook for the lesson.
  • It will be a digital task.
  • It will be a review of the previous day.
  • It will be state testing review.
  • It will be college readiness review.
  • It will be spiral review.
  • It will be a writing task.
  • It will be a seasonal math task.

Once you lock in that purpose, you can hunt down the material. You need to think about how much time you want to spend on the bell ringer in class. That will help determine how many questions you want to have. I’ve listed some ways to come up with the problems:

  • Search real-life examples so the problems have meaning.
  • Use Desmos activities and spread them out over a week.
  • Write questions that are similar to the homework.
  • Use released test questions from your state tests or from college entrance exams.
  • Grab problems out of the math book at the end of units for spiral reviews.
  • Use AI generated questions. Beware! AI is not always great with math.

Now that you know your purpose and where your material is coming from, what format do you want to use? I’ve done different things, but one of my favorites is a three question approach where the first two questions scaffold for the third question. I’ve used this format in my ACT Bell Ringers as well as my SAT Bell Ringers. Day 26 from the SAT Bell Ringers is seen below:

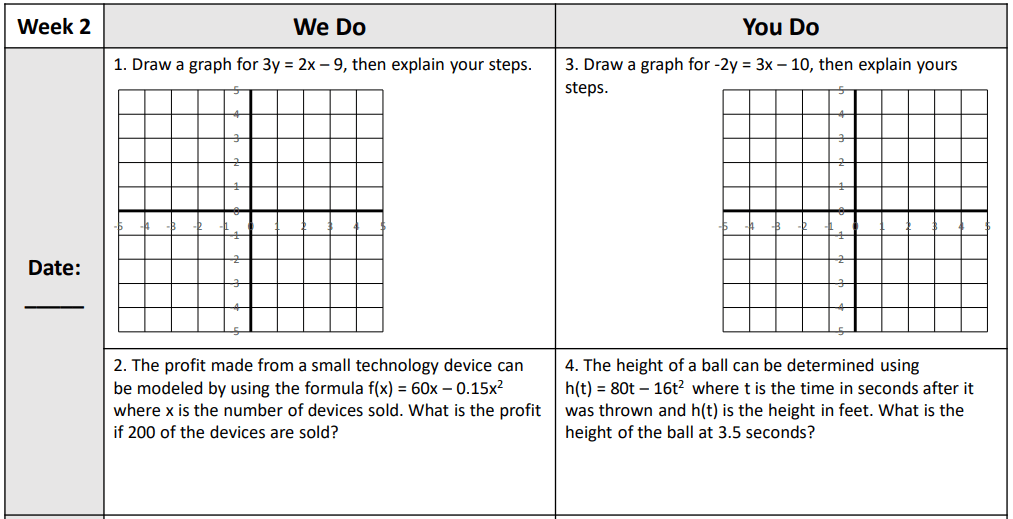
Another option is “We Do, You Do”. Together with the class, the teacher works through 1 and 2 and then lets the students work by themselves on 3 and 4. In this format, the teacher will begin class working the problems. When students work the other two, she can go do her attendance and other tasks. This approach is good when you have students that have a hard time starting. The example below is from my Algebra Review Bell Ringers.

Recently, I’ve been developing a new style of bell ringers designed with differentiation in mind. Instead of every student working through the same set of problems, this format allows students to choose from multiple levels of challenge based on their confidence and readiness that day.

This approach keeps all learners engaged—whether they need a little extra support or are ready to stretch their thinking. It also builds student independence, since they’re making decisions about how to approach the task. These differentiated bell ringers aren’t uploaded just yet, but they’re on the way. I’m excited to share them soon!

Your Bell Ringer Investment

Most of us do not want to spend our precious teacher planning period on bell ringers, so we end up working on it at home. If you decide to create these bell ringers yourself, then by all means save them so you have them for the next year. Make your time investment work for you in the future.

If you decide that recreating the wheel is not for you, then you can look at what I have. I’ve bundled up my most-used bell ringers from over the years to save others some prep time. Whether it’s Geometry, Algebra, or even a sprinkle of Trig, there’s plenty of things to choose from. Check out the resource after the final paragraph. You can look at the individual items and purchase them separately too.

In closing, the journey with bell ringers is an exploration of balancing their benefits and challenges. As educators, we adapt and refine our approach, always seeking the best ways to engage our students. Whether you’re harnessing the power of purpose-driven bell ringers, navigating their quirks, or even deciding to take a break when necessary, remember that your dedication to creating a meaningful learning experience remains at the heart of it all. With purpose as your guide, you’re well on your way to transforming those initial moments into impactful stepping stones towards an enriched classroom experience. Keep up the incredible work, and keep those bell ringers ringing with purpose!