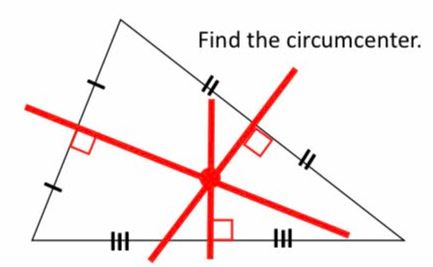
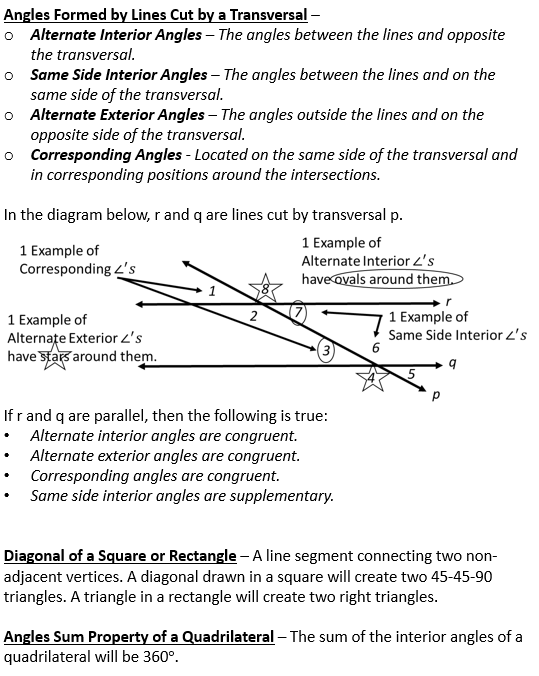
If you’ve ever told a student to show their work and been met with blank stares, scribbled-down numbers, or complete avoidance, you’re not alone. The truth is, many students don’t actually know what show your work means—or why it matters. To them, it sounds like just another rule, a hoop to jump through. But what if we reframed it?
The key is helping students see that showing their work isn’t about writing things down just because we said so—IT’S ABOUT MAKING THEIR THINKING VISIBLE! It’s about leaving a trail so they can check their reasoning, catch mistakes, and explain their process. And sometimes, the phrase show your work just doesn’t connect.
So, let’s rethink the way we ask students to document their thinking. Here are 30 different ways to say ‘show your work’ that might resonate more with your students:
Process-Oriented Phrases
- Document your thinking.
- Make mathematical notes.
- Write down your thought process.
- Track your steps.
- Show how you figured it out.
- Record your strategy.
- Map out your solution.
- Make your thinking visible.
- Break it down step by step.
- Illustrate your reasoning.
Student-Centered Language
- Convince me your answer makes sense.
- Tell the story of how you solved it.
- What would you write to teach someone else?
- Create a roadmap for your brain.
- Explain your approach in a way a friend would understand.
- Help me see what’s going on in your head.
- Write it in a way future-you will understand when you check your work.
- If you got stuck, what steps did you take before that?
- How can you prove your answer is correct?
- Would someone else be able to follow your thinking?
Visual/Creative Approaches
- Sketch your solution.
- Draw a diagram to support your answer.
- Use arrows or highlights to show key steps.
- Make a quick explainer box.
- Write a one-minute summary of what you did.
- Turn it into a “math comic strip.”
- Use colors to separate different parts of your thinking.
- Write a math journal entry about this problem.
- Make a checklist of the steps you took.
- Explain it in a way you’d post on social media (but keep it math-related!).
Why This Matters
When students hear show your work, they often think we’re asking for a long, tedious process that just slows them down. But when we shift the language to focus on thinking, reasoning, and problem-solving, it becomes more meaningful.
Try using some of these alternative phrases in your classroom and see how your students respond. You might just find that showing their work becomes something they actually understand—and maybe even value.
What are your favorite ways to get students to document their thinking? Do you like any of the ones above? Share in the comments!
Bell ringers are a great place to have students demonstrate they know how to show work or make their reasoning visible. The bundle below has 144 days-worth of bell work problems. Click on the resource to see more details.